
◎承芳老師
六年級的孩子們正在學雞兔同籠的問題,為了讓孩子們掌握解題方法,我們研究了許多問題,除了把腳數不同的動物關到同個籠子之外,我們也討論各種變型題。
有一回,要研究的問題是:
小明有 10元及 50元硬幣 20 枚,共值 840 元,請問兩種硬幣各有多少枚?
孩子們一致同意,先假想20枚硬幣都是50元,而不選擇假想20枚硬幣都是10元。
「因為比較接近840元啊!」孩子們說。
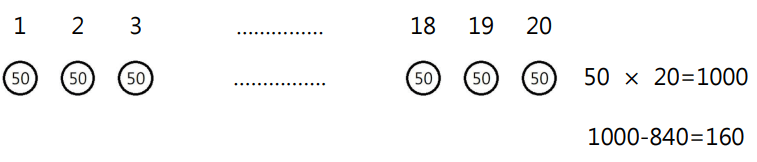
照我們的假設,20枚50元應該要有1000元;
但實際上只有840元,多了160元,
表示有些硬幣應該是10元,而不是50元。
那到底有幾個10元硬幣呢?
如果把1枚50元硬幣替換為10元硬幣,硬幣總數還是維持20枚,但總金額會減少40元;要把多算的160元都減完,就要把4枚50元替換為4枚10元。

這個方法練過好幾次了,多數孩子很熟悉,計算跟說明都難不倒他們。
這時,有個平時不太發言的小孩說:「可是,我不是這樣算的。」
大家都很好奇,這種複雜的問題還有什麼辦法呢?
那個小孩說:「50元硬幣一定湊不出840元啊,所以其中的40元一定是10元硬幣組成的,那就確定有4枚10元硬幣。」

聽到這裡,有幾個小孩露出驚喜的表情,也有孩子一臉狐疑。
這位小孩繼續說:「然後再想幾個50元會湊成800元,就是16個啊。」
全班聽懂之後,齊聲向我抱怨:「這麼簡單!怎麼不早說。」想出這個辦法的小孩則是非常高興。
實際上,這一題,因為數字很剛好,所以這個想法很快就能找到答案,要是換個數字,就不見得這麼好用。
為了讓孩子們體會這一點,我請大家接著想,要是題目改成:「小明有 10元及 50元硬幣 20 枚,共值 720 元,請問兩種硬幣各有多少枚?」
馬上有人依樣畫葫蘆,說:「那有2枚10元,因為50元硬幣湊不出20元。」
另一位接著說:「14枚50元可以湊成700元。」
好幾個小孩都發出讚嘆,直說這個方法真的很快。
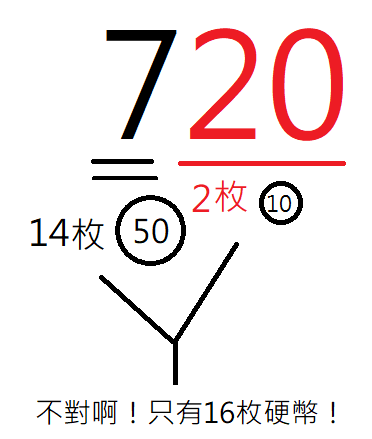
突然,有人說:「不對啊!這樣總共只有16枚硬幣!!」
這才意識到,大家很得意的結果並不是答案。
這個發現讓大家從興奮回歸平靜,繼續想著:那該怎麼辦?
不久,有個聲音傳出:「那把50元換成10元,硬幣就會變多。」
對唉!拿1個50元可以換到5個10元。每換一次錢,就少1枚50元,多5枚10元,總金額不變,硬幣總數多4枚。
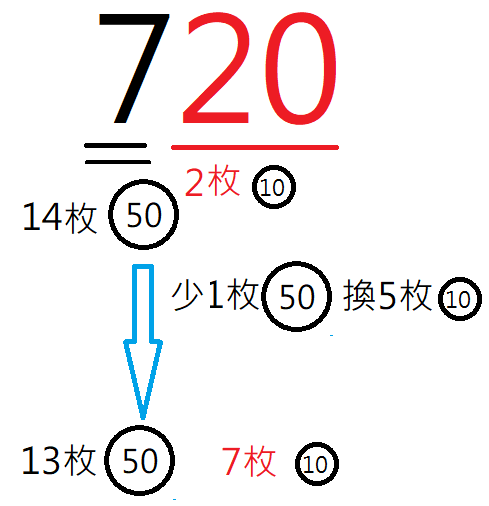
想通這一點,小孩們又七嘴八舌地講起該怎麼換錢以符合題目的條件。
最後,一個小孩下了結論:
原來的方法,是先符合20枚,再符合總金額;後來的方法,是先符合總金額,再符合20枚。其實都差不多啦!
結論,是孩子下的,老師呢?
笑看這個過程,並欣賞著孩子們起起伏伏的各種反應。


